ハノイの塔

問題：paiza | S062:パズルの手助け

パイザさんはハノイの塔というパズルで遊んでみることにしました。このパズルには、N 枚の円盤と 3 つの杭が刺さっているプレートを用います。

N 枚の円盤をそれぞれ円盤 1、円盤 2、……、円盤 N と呼ぶことにします。これらの円盤の大きさはそれぞれ相異なり、小さい順に番号が付いています。

プレートに刺さっている 3 つの杭を、左から順に杭 A、杭 B、杭 C と呼ぶことにします。このとき、ハノイの塔は以下のルールで遊ぶパズルです。

・はじめに、杭 A に円盤を下から大きい順に N 個重ねておく。
・円盤を 1 枚ずつ動かし、最終的に杭 C に円盤を下から大きい順に N 個重ねることを目指す。
・ただし、円盤を移動するときは、以下の条件のいずれかが成り立っていないといけない。
　・移動先の杭に円盤が 1 枚も置かれていない。
　・移動先の杭にすでに置かれている円盤の大きさよりも、移動させようとしている円盤の大きさの方が小さい。

たとえば、 3 つの円盤を使ってハノイの塔を遊ぶ場合、次の図のように動かすと、7 回円盤を移動させることですべての円盤を杭 C に移動させることが出来ます。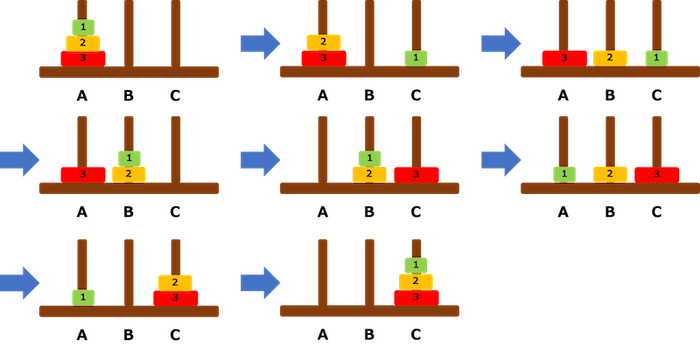

パイザさんはしばらくハノイの塔で遊んでいたのですが、どうにもうまく杭 C にすべての円盤を移動させることが出来ません。そこで、あなたは自分の現在の盤面の様子を入力すると、そこから最短で何回円盤を移動させることでで杭 C にすべての円盤を移動させることができるかを求めるプログラムをパイザさんのために作ってあげることにしました。

パイザさんの遊んでいたハノイの塔の円盤の枚数と、それぞれの円盤がどの杭に置かれているかという情報が与えられたとき、その状態から杭 C にすべての円盤を移動させるために必要な円盤の移動回数の最小値を求めるプログラムを作成してください。

たとえば、入力例 1 の場合、パイザさんは 5 枚の円盤を用いてハノイの塔をプレイしており、現在の盤面では、
・円盤 1 が杭 B に、
・円盤 2 が杭 B に、
・円盤 3 が杭 A に、
・円盤 4 が杭 C に、
・円盤 5 が杭 C に

あります。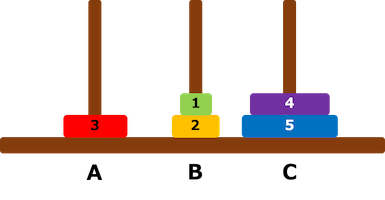

次の図の手順で円盤を移動させていくことで、この状態から 4 回の円盤の移動ですべての円盤を杭 C に移動させることができます。移動回数 3 回以下ですべての円盤を杭 C に移動させることは出来ないため、この場合は 4 と出力します。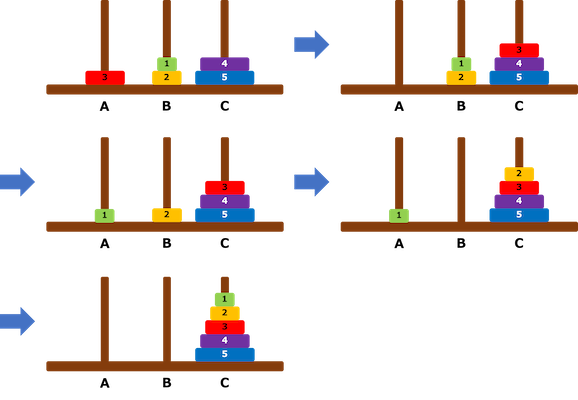

入力される値
入力は次のフォーマットで与えられます。
N
c_1
c_2
…
c_N

・1 行目に、ハノイの塔に使われている円盤の枚数を表す整数 N が与えられます。
・続く N 行のうちの i 行目 (1 ≦ i ≦ N) には、i 番目の円盤がどの杭にあるのかを表す文字 c_i が与えられます。

文字列は標準入力から渡されます。標準入力からの値取得方法はこちらをご確認ください
期待する出力
杭 C にすべての円盤を移動させるために必要な円盤の移動回数の最小値を出力してください。
末尾に改行を入れ、余計な文字、空行を含んではいけません。
条件
すべてのテストケースにおいて、以下の条件をみたします。
・1 ≦ N ≦ 50
・c_i は “A”, “B”, “C” のいずれかの文字 (1 ≦ i ≦ N)
・入力で与えられる盤面は、ハノイの塔のルールに違反していない

言語別実行時間制限の詳細は こちら をご確認ください。
入力例1
5
B
B
A
C
C
出力例1
4
入力例2
12
A
B
C
A
C
B
A
C
B
B
A
A
出力例2
3925

解決

どちらかというと、この問題は分割統治法で解決されました。
具体的な考え方はソースコードのコメントのように書いてあります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import java.util.*;

public class Main {
    static final int A_MARK = 1 << 0;
    static final int B_MARK = 1 << 1;
    static final int C_MARK = 1 << 2;

    static final int FULL_MARK = A_MARK | B_MARK | C_MARK;

    static final int MAX_N = 50 + 1;

    static long dp[] = new long[MAX_N];

    static long proc(List<Integer> list, int N, int target) {
        int posOfBiggest = list.get(N - 1);

        //再帰の終わりの場合
        if (N == 1) {
            if (posOfBiggest == target) {
                return 0;
            }
            return 1;
        }

        //もし最大の円盤が正しい位置に置かれていたら、
        if (posOfBiggest == target) {
            return proc(list, N - 1, target);
        }

        int newTarget = FULL_MARK - posOfBiggest - target;
        //余った円盤を新しい位置に移動させる
        long ret = proc(list, N - 1, newTarget);
        //最大の円盤は目標の位置に移動すると、１ステップが掛かります
        //そして、最大の円盤を除いた他の円盤は、新しい位置から目標の位置に移動するのに、dp[N - 1]ステップが掛かります。
        return 1 + ret + dp[N - 1];
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();

        List<Integer> lists = new ArrayList<>();
        sc.nextLine();
        for (int i = 0; i < N; i++) {
            String pos = sc.nextLine();
            lists.add(1 << (pos.charAt(0) - 'A'));
        }
        dp[1] = 1L;
        for (int i = 2; i < MAX_N; i++) {
            dp[i] = 1 + (2 * dp[i - 1]);
        }
        long ret = proc(lists, N, C_MARK);
        System.out.println(ret);
    }
}